We zijn gewend dat roeiers in de dubbel twee of dubbel vier precies elkaars beweging volgen. Toch zijn er goede argumenten om te denken dat asynchroon roeien tot betere resultaten leidt. Wat doe je als je alle menselijke factoren uit wil schakelen? Dan laat je ro(w)bots roeien. Maar zelfs dan blijft het de vraag wat nou werkelijk beter is.
Lees verder Rowbots: Het mysterie rond (a)synchroon roeienTag: biomechanica
Roeien: Het meten van geleverd vermogen
Bij sporten zoals wielrennen en roeien wordt het vermogen dat de sporter levert gemeten en gebruikt voor analyses en trainingen. Normaal gesproken wordt er bij roeien alleen rekening gehouden met de kracht die de roeier uitoefent op de roeiriem. De roeier levert echter ook vermogen door kracht te zetten op het voetenbord. De impact hiervan is berekend en gemeten door Lotte Lintmeijer, Mathijs Hofmijster en een team van de VU met behulp van 13 sensoren op roeiers. Zoveel sensoren is echter duur en onpraktisch. Hun vraag aan Youssef El Bouhassani en mij: Kan het ook met minder sensoren, en zo ja, welke sensoren moet je dan selecteren? Drie sensoren lijken al een goed resultaat te geven.
Vorig jaar november organiseerde de HvA een conferentie over Sport en Data Science. Daar moest ik natuurlijk bij zijn. Youssef El Bouhassani, data scienist op de HvA, sprak daar. Hij zei tegen de zaal dat als ze een dataset hadden en een vraag, ze naar hem toe konden komen. Dat deed Lotte, en daar stond ik toevallig weer naast. En zo ontstond een mini-project op het gebied van roeien en het selecteren van sensoren.
Normaliter wordt het vermogen dat een roeier levert alleen berekend aan de hand van de kracht die hij op de roeiriem uitoefent en de snelheid van de riem. Met behulp van een gedachte-experiment laten Lotte en Mathijs in dit artikel zien dat dat niet klopt, en dat een roeier ook vermogen levert via het voetenbord. Stel je voor dat een roeier in een boot zonder roeispanen met de voeten vast aan het voetenbord naar voren en naar achteren beweegt. De boot zal dan naar achteren en naar voren bewegen. De roeier levert hierbij vermogen, want hij moet waterweerstand overwinnen. Met behulp van simulaties op basis van (bio)mechanische vergelijkingen in het artikel, laten de auteurs zien dat wanneer je het geleverde vermogen van een roeier bepaalt op basis van alleen de kracht die hij op de handen levert, je het echte geleverde vermogen met meer dan 10% onderschat. Ook laten ze zien dat de extra component berekend kan worden aan de hand van de versnelling van het massamiddelpunt van de roeier. En dat is fijn, want die is betrouwbaarder te meten dan de kracht die op het voetenbord wordt uitgeoefend. Het leuke is dat het effect met relatief eenvoudige natuurkunde aan te tonen is. Toch kostte het me wel flink wat moeite om de formules (enigszins) te doorgronden. Er komt ook al een flinke discussie over op gang in “roeiersland”. Mijn natuurkundehart ging er in ieder geval weer even sneller van kloppen. Wil je precies weten hoe het zit, open dan zeker het artikel.
De vervolgstap was om deze onderschatting van het daadwerkelijke geleverde vermogen te meten in de praktijk. Om de versnelling van het massamiddelpunt van de roeier te bepalen werden er 13 sensoren op de deelnemende roeiers geplakt. Maar voordat ze dat op een boot op het water deden, hebben ze eerst onderzocht of de sensoren hun werk goed doen door een roeiapparaat op een “krachtenplatform” te zetten. Het krachtenplatform kan precies meten welke krachten de roeier uitoefent op het apparaat. Met deze krachten kan de versnelling van het massamiddelpunt van de roeier worden bepaald. Deze gemeten versnelling werd in het experiment gezien als de “werkelijk” gemeten versnelling van het massamiddelpunt van de roeier (“de gouden standaard”). Om te kijken hoe goed de 13 sensoren de versnelling van het massamiddelpunt van een roeier kunnen meten, werd deze versnelling vergeleken met de gouden standaard.
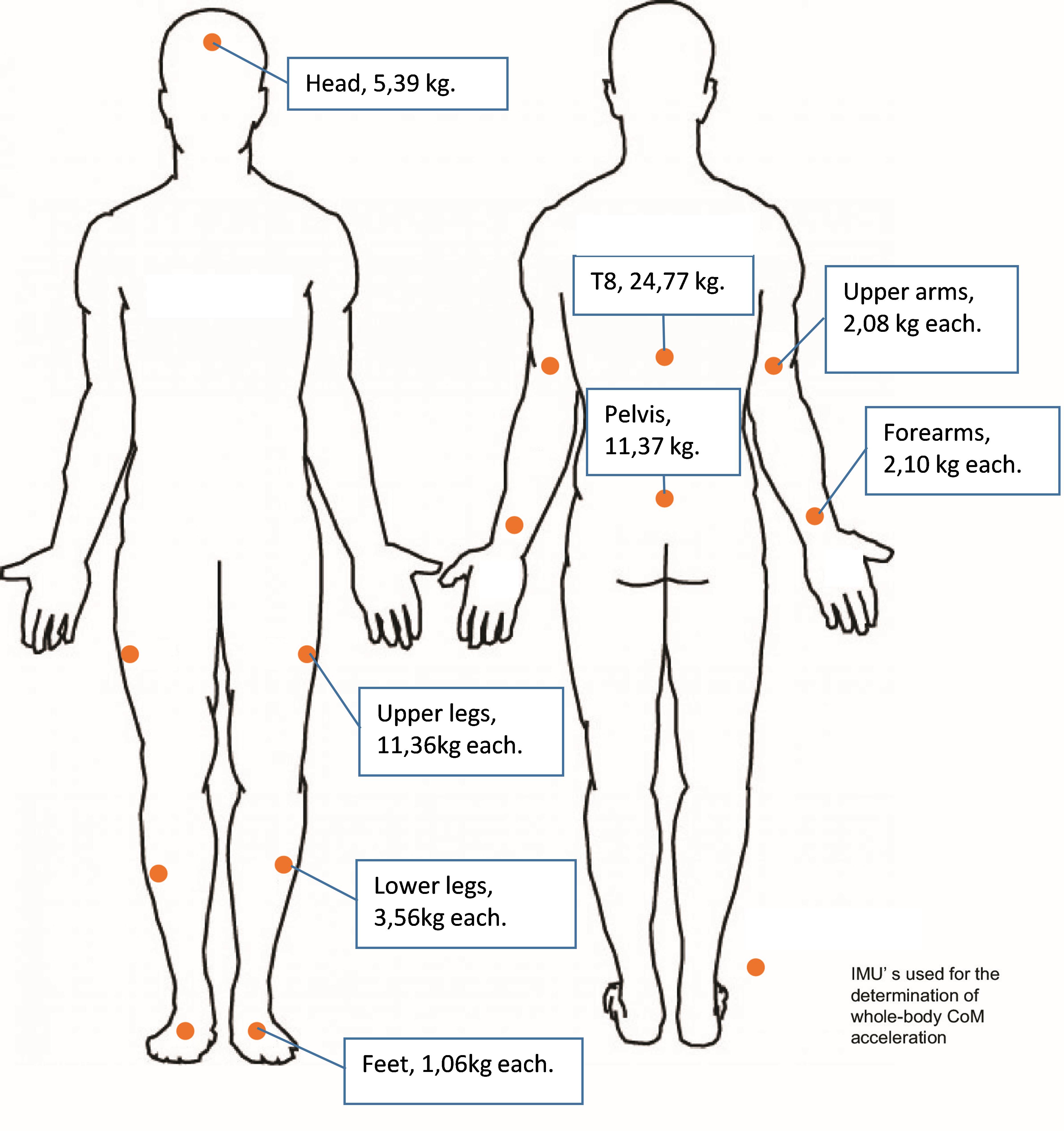
De 13 sensoren meten de versnelling en vertraging van specifieke lichaamsdelen (hoofd, benen, armen, voeten, bekken, romp). De versnelling van het massamiddelpunt van de roeier (a_roeier) kan berekend worden door de versnelling per sensor (a_i), te wegen met de massa van het lichaamsdeel dat bij de sensor hoort:

Hieronder is te zien op welke plekken de sensoren zaten, en wat de gemiddelde geschatte massa is van het bijbehorende lichaamsdeel:
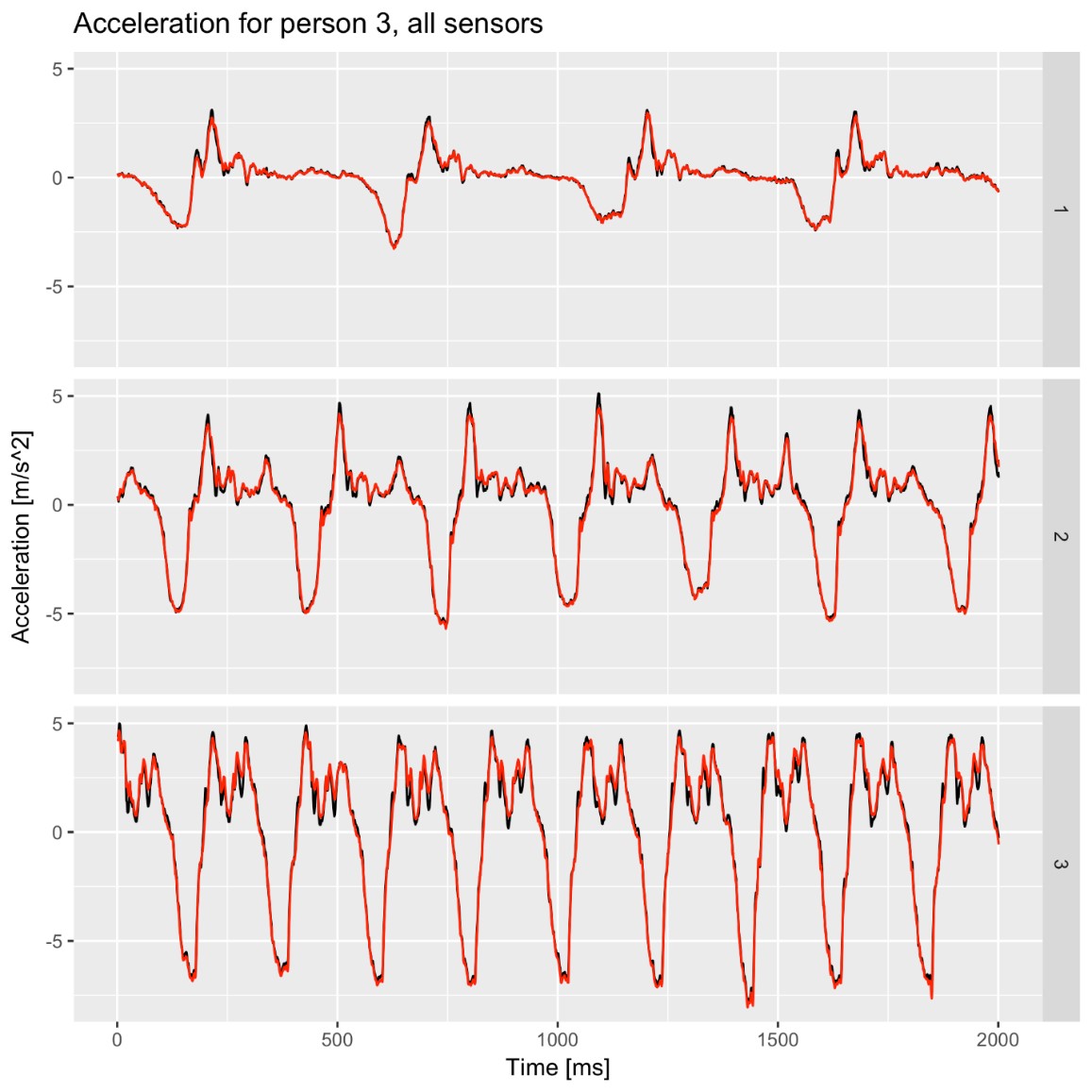
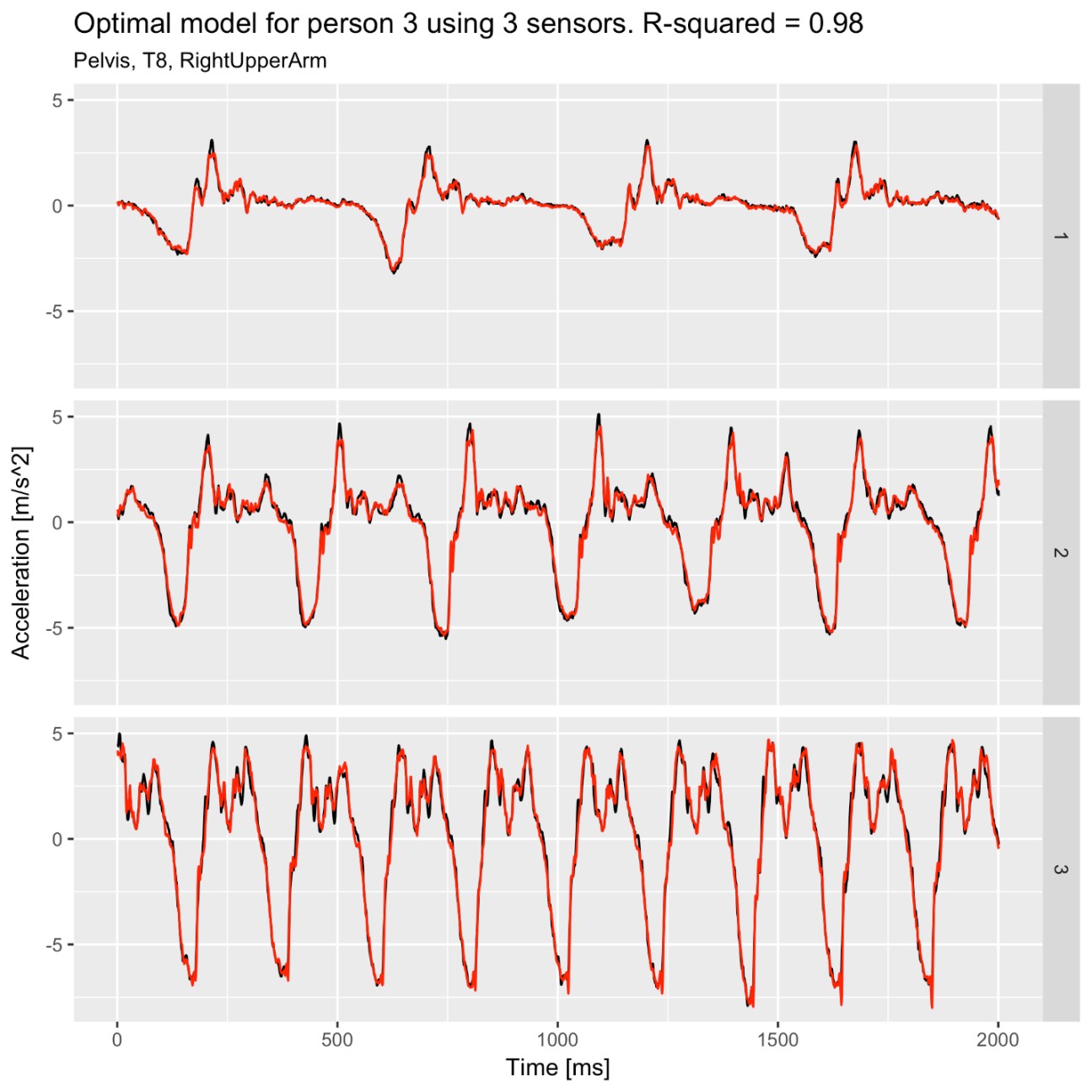
Negen proefpersonen hebben met drie verschillende frequenties geroeid. De data op basis van de sensoren is vergeleken met de data van het krachtenplatform, en kwam goed overeen. De versnelling van het massamiddelpunt van de roeier kan dus goed worden bepaald met de sensoren. Hieronder is voor proefpersoon 3 te zien wat de versnelling van zijn massamiddelpunt was in de tijd. De zwarte lijn geeft de meting van het krachtenplatform weer, de rode lijn is gebaseerd op de sensoren.
De vraag van Lotte en Mathijs aan ons was: Kun je de versnelling van het massamiddelpunt van de roeier ook nauwkeurig meten met minder sensoren? En zo ja, welke moet je dan kiezen? Het opplakken van sensoren is duur en onpraktisch. Het zou dus fijn zijn om vervolgmetingen uit te kunnen voeren met minder sensoren. Om die vraag te beantwoorden hebben we in eerste instantie gekeken naar de correlatie tussen de versnellingen van de verschillende lichaamsdelen van drie proefpersonen. Als twee sensoren een hoge onderlinge correlatie hebben, dan zou je een van de twee weg kunnen laten. De correlatie is berekend door voor de 13 sensoren de data van alle proefpersonen bij alle trials achter elkaar te plakken, en daar de correlatie tussen te berekenen. Dat leidt tot de volgende correlatiematrix:

We zien dat er clusters zijn van sensoren die een hoge onderlinge correlatie hebben. Die zijn vaak ook niet heel verrassend. Zo bewegen de boven- en onderarmen vaak dezelfde kant op, en de boven- en onderbenen ook. De benen hebben een hoge correlatie met de romp en het hoofd. De linker- en rechtervoet hebben een lage correlatie met alle andere lichaamsdelen.
Als eerst hebben we gekeken of we uit elk cluster één sensor kunnen gebruiken zodat elke sensor nieuwe informatie toevoegt. Dat zou de optimale keuze kunnen zijn bij vier sensoren. Dat is echter niet het geval. De voeten hebben weliswaar een lage correlatie met alle andere lichaamsdelen, maar hebben ook een laag gewicht. Ze dragen daardoor weinig bij aan de versnelling van het massamiddelpunt van de roeier. De sensor op de pelvis (bekken) en de T8 (romp) hebben een hoge onderlinge correlatie, maar vertegenwoordigen beiden een relatief hoog gewicht. Het is dus niet verstandig om één van de twee zomaar weg te laten. Hoe komen we dan tot de optimale keuze? We hebben gekozen voor bruut (reken)geweld. Stel je wil een optimale keuze maken bestaande uit drie sensoren. Voor alle mogelijke manieren waarop je drie uit 13 sensoren kunt selecteren (286 combinaties), kun je een regressieanalyse uitvoeren, en bepalen hoeveel procent van de variantie in de beweging van het massamiddelpunt van de roeier verklaard wordt door de combinatie van die drie sensoren. Uit die regressie volgt ook met welke coëfficienten de versnelling van de sensoren vermenigvuldigd moeten worden om de versnelling van het massamiddelpunt van de roeier te berekenen. Als alle 13 sensoren worden gebruikt is de coëfficient in theorie gelijk aan het procentuele gewicht van het bijbehorende lichaamsdeel. Bij minder sensoren is dat niet meer het geval. De combinatie die de hoogste verklaarde variantie oplevert kiezen we als de optimale combinatie. Dit levert de volgende resultaten op:
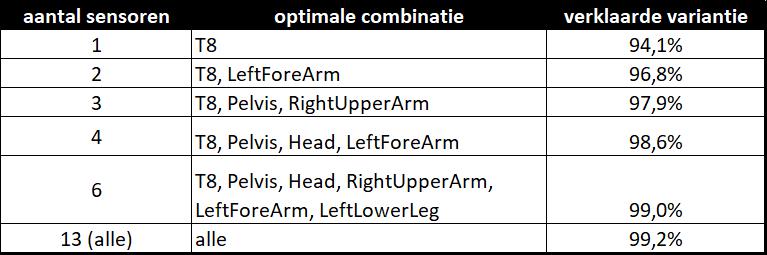
Als je alle sensoren gebruikt, lijkt de data op basis van de sensoren erg op de gemeten versnelling via het krachtenplatform. Ruim 99% van de variantie in de data wordt verklaard door de 13 sensoren. Als je slechts één sensor gebruikt, zou je die ter hoogte van de T8 moeten plakken. Dat is een wervel ongeveer halverwege de ruggengraat. Je verklaart dan 94.1% van de variantie. Bij twee sensoren zou je ook een sensor op de arm toe moeten voegen. Uit de analyse komt dat dit de linker bovenarm moet zijn. Waarschijnlijk maakt het qua verklaarde variantie weinig uit of dit nu de linker- of rechterarm is. Bij drie sensoren komt er ook een sensor op het bekken (Pelvis) bij. Hieronder is de versnelling op basis van drie sensoren vergeleken met die van het krachtenplatform. De verklaarde variantie is iets lager dan wanneer je alle sensoren gebruikt, maar met het blote oog is het verschil met 13 sensoren bijna niet te zien. Voor het huidige onderzoek lijken 3 sensoren dus meer dan voldoende.
De resultaten van de metingen op het water zijn gepubliceerd in dit artikel. Ook op basis van metingen blijkt dat de onderschatting van het geleverde vermogen door het versnellen en vertragen van het massamiddelpunt van de roeier rond de 12% ligt, en dus niet zomaar genegeerd kan worden. Vervolgonderzoek kan wellicht met drie sensoren. Voor het zo ver is, zou het goed zijn om de bovenstaande analyse uit te breiden. Nu zijn alle proefpersonen en trials op één hoop gegooid. Het zou interessant zijn om te kijken of er verschillen zitten in de optimale selectie als de analyse per persoon en/of per trial zou worden uitgevoerd, en hoe voorspellend deze resultaten zijn voor de andere 6 proefpersonen. Nog een interessant punt: Als je 13 sensoren gebruikt, wordt de versnelling van een sensor gewogen met het gewicht van het bijbehorende lichaamsdeel. Bij minder sensoren volgt de weging van een sensor uit de resultaten van de regressie (een soort calibratie). Daar zit dan geen directe fysische betekenis aan. Het zou interessant zijn om te kijken hoe stabiel die coefficiënten zijn, en of er een fysische betekenis aan te koppelen is.
Bronnen:
Lotte L. Lintmeijer, Mathijs J. Hofmijster, Guido A. Schulte Fischedick, Patrick J. Zijlstra & A. J. “Knoek” Van Soest (2018) Improved determination of mechanical power output in rowing: Experimental results, Journal of Sports Sciences, 36:18, 2138-2146, DOI:10.1080/02640414.2017.1367821
Mathijs J. Hofmijster, Lotte L. Lintmeijer, Peter J. Beek & A. J. Knoek van Soest (2018) Mechanical power output in rowing should not be determined from oar forces and oar motion alone, Journal of Sports Sciences, 36:18, 2147-2153, DOI:10.1080/02640414.2018.1439346
https://rowe.rs/the-flaw-in-current-power-output-calculations/

 Twee roeiers die deelnemen aan het onderzoek, met sensoren op hun lichaam.
Twee roeiers die deelnemen aan het onderzoek, met sensoren op hun lichaam.
De wetenschap achter de 200 meter sprint
In het tijdschrift STAtOR heb ik een vervolgonderzoek gepubliceerd. Het artikel is hier te vinden.
Augustus vorig jaar werd Dafne Schippers wereldkampioen op de 200 meter sprint. Nu “we” meedoen op deze afstand, neemt de belangstelling toe. Zou ze deze zomer ook Olympisch kampioen kunnen worden? Ook door een natuurkundige en wiskundige bril is deze afstand interessant. De wetenschap heeft van alles te zeggen over de invloed van hoogte, luchtdruk, wind, en het effect van de laan waarin de atleten loopt.
De 200 meter
Bij baanatletiek lopen atleten op een 400 meter baan. De baan bestaat uit twee rechte stukken van ongeveer 100 meter, en twee bochten. De atleten lopen naast elkaar in 4 tot 9 lanen. De binnenste laan, laan 1, loopt een kortere bocht dan de buitenste laan. Daarom starten de atleten niet naast elkaar, maar mag de buitenste laan verder naar voren starten, zodat ze als ze over de finish komen, allemaal precies 200 meter hebben afgelegd.
Op een groot toernooi worden er eerst series gelopen, waar de sprinters zich kunnen plaatsen voor de halve finales en de finale. In de eerste serie krijgen de atleten willekeurig een laan toegewezen. Atleten die de snelste tijd hebben gelopen in de series, starten in de volgende ronde in de binnenste lanen (4 en 5). Het is voordelig om een ruimere bocht te lopen, want dit kost minder kracht. Het is dus nadelig om in laan 1 te starten. Bij indoor atletiek is de baan 200 meter in plaats van 400 meter, en lopen de atleten dus een volle ronde. Het nadeel van een krappere bocht is hier zo groot, dat deze afstand bij indoortoernooien van het programma is gehaald.

De beste tijd ooit?
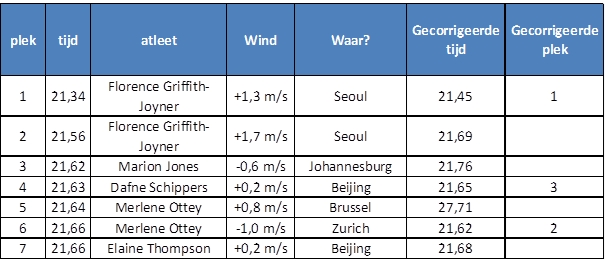
Dafne Schippers werd vorig jaar niet alleen wereldkampioen, maar werd met 21,63 seconde ook de derde snelste atlete ooit. Alleen Florence Griffith-Joyner (21,34) en Marion Jones (21,62) waren sneller. Wat zijn de ideale omstandigheden om een snelle tijd te lopen? Het is vanwege de bocht dus voordelig om in de buitenste laan te starten. Maar ook de luchtdruk speelt een rol. Hoe hoger de luchtdruk, hoe hoger de luchtweerstand, en hoe moeilijker het is om een snelle tijd te lopen. Dit effect is ook heel duidelijk bij schaatsen. Daar worden wereldrecords altijd gereden op hooglandbanen zoals Calgary en Salt Lake City, waar de luchtdruk laag is. Omdat het zo goed als onmogelijk is om dezelfde tijd te rijden op een laaglandbaan, zijn hier zelfs officieuze aparte wereldrecords voor. Ook helpt het natuurlijk als je wind mee hebt. Bij atletiek is een wereldrecord daarom pas officieel als de windsnelheid minder dan 2 meter per seconde is. En vanwege het voordeel van een hoogland baan, komt er bij een baan die hoger dan 1000 meter boven zeeniveau ligt een A achter het wereldrecord te staan.
Jonas Mureika, een professor natuurkunde in Los Angeles, heeft een model ontwikkeld waarmee hij het effect van luchtdruk, mee- of tegenwind en de startlaan heeft geschat. De kern van het model is een formule die je misschien nog kent van de natuurkundelessen van de middelbare school: F=m*a. Kracht is massa keer versnelling, de beroemde tweede wet van Newton. Een sprinter oefent kracht uit, om te versnellen, en zo snel mogelijk te lopen. Er zijn ook krachten buiten de atleet die meewerken of tegenwerken. De luchtweerstand moet overwonnen worden, en hoe hoger de luchtdruk, hoe groter deze tegenkracht. Ook tegenwind kan tegenkracht geven, en meewind een extra duwtje in de rug. Als laatste is ook het effect van de bocht in een kracht te vatten. Als je de bocht ziet als een halve cirkel, moet de atleet een kracht uitoefenen richting het middelpunt van de cirkel, om de bocht te lopen, de middelpuntzoekende kracht. Hoe kleiner de straal van de cirkel is, hoe groter deze kracht is, en daarom is het nadelig om de binnenbocht te lopen. Op zijn website kun je de 200 meter tijd bepalen die corrigeert voor deze drie effecten. Op basis daarvan zou je een nieuwe ranglijst van beste atletes ooit kunnen maken. Dafne Schippers blijft dan op de derde plek staan, alleen moet Marion Jones haar tweede plek afstaan aan Merlene Ottey. Jones liep 21,62 in Johannesburg, en Ottey 21,66 in Zurich. Ottey had meer tegenwind dan Jones, Zurich ligt op 400 meter hoogte, en Johannesburg op 1700 meter. Twee factoren waardoor de tijd van Ottey naar beneden wordt bijgesteld, en die van Jones naar boven.
Statistiek en het effect van de startlaan
(inmiddels heb ik vervolgonderzoek gedaan naar het effect van de startlaan. De link naar dat artikel is bovenaan te vinden).
De tijd die een atleet loopt wordt dus beïnvloed door de hoogte, wind en de startlaan. De hoogte en de wind zijn voor alle atleten in een wedstrijd hetzelfde. Maar het effect van de startlaan geeft de atleet in de buitenste laan een voorsprong op de atleet die in de binnenste laan start. Is dit ook terug te zien in de resultaten op een wereldkampioenschap? In de eerste ronde krijgen de atleten willekeurig een startlaan toegewezen. Het zou dan zo moeten zijn dat atleten in laan 8 zich significant vaker voor de volgende ronde kwalificeren dan atleten in laan 1. Om dat te testen bekijken we alle series van wereldkampioenschappen atletiek outdoor vanaf 1991, en de Olympische Spelen vanaf 2000. Atleten die gediskwalificeerd werden, of de finish niet bereikten zijn weggelaten.
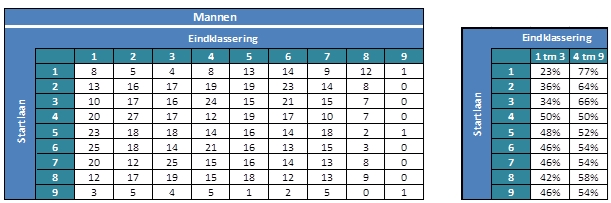
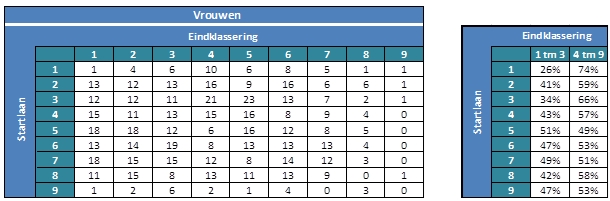
In de figuren hieronder is voor alle combinaties van startlaan en eindklassering te zien hoe vaak die voorkwam. Zo zijn er bijvoorbeeld 23 mannen geweest die startten in laan 5 en als eerste eindigden. En waren er 5 vrouwelijke atletes die startten in laan 5 en als 8e eindigden. Bij de meeste kwalificaties plaatsen de eerste drie atleten zich voor de volgende ronde. We kunnen nu uitrekenen hoe vaak een atleet zich kwalificeerde, afhankelijk van de startlaan. En dan zien we opmerkelijke verschillen. Bij de mannen kwalificeert maar 23% van de atleten in laan 1 zich, tegenover bijvoorbeeld 50% in laan 4. Ook bij de vrouwen valt op dat atletes in laan 1 zich minder vaak plaatsen voor de volgende ronde.
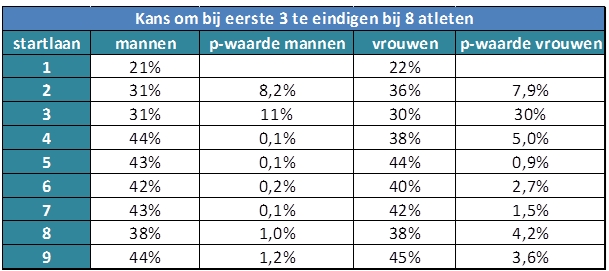
Het kan natuurlijk zijn dat dit door toeval wordt veroorzaakt. Ook starten niet in elke serie evenveel atleten. Een manier om te testen of het verschil op toeval kan berusten is door een zogenaamd Generalized Linear Model te schatten. Hierbij corrigeren we eerst voor het aantal atleten dat meedoet aan een serie. Vervolgens schat het model de kans dat een atleet bij de eerste drie eindigt, afhankelijk van de startlaan, als er acht atleten mee zouden doen. Ook bepaalt het model hoe groot de kans is dat verschillen op toeval berusten. In de tabel hieronder zijn de resultaten te zien. Als er geen effect van startlaan was, zou de kans om bij de eerste drie te eindigen altijd ongeveer 3/8=37,5% moeten zijn. In laan 1 ligt deze kans nog steeds een stuk lager, zowel voor mannen als voor vrouwen. Ook in laan 2 en 3 ligt de kans om bij de eerste drie te eindigen onder de 37,5%. De kolom met de p-waarde berekent de kans dat verschillen tussen startlanen door toeval ontstaan. Hierbij wordt een startlaan altijd vergeleken met laan 1. Meestal wordt een grens van 5% gehanteerd. Pas als de p–waarde kleiner is dan 5%, gaan we er vanuit dat verschillen niet op toeval berusten. We noemen het effect dan statistisch significant. Voor laan 2 en 3 is de kans dat een atleet zich plaatst niet significant anders ten opzichte van laan 1. Voor laan 5 tot en met 9 wel. De startlaan heeft dus een statistisch significant effect op de kans dat een atleet zich plaatst voor de volgende ronde.
Conclusie
De tijd die een atleet loopt op de 200 meter wordt beïnvloed door wind, hoogte en de laan waarin de atleet start. Op basis van een natuurkundig model kunnen tijden op verschillende hoogtes en bij verschillende windsnelheden met elkaar vergeleken worden. Marion Jones moet haar positie als tweede snelste vrouw ooit dan afstaan aan Merlene Ottey. Starten in de binnenste laan levert een nadeel op, dat statistisch aangetoond kan worden.
Mureika, J. R. “Modeling wind and altitude effects in the 200 m sprint.” Canadian Journal of Physics 81.7 (2003): 895-910.
Mureika, J. R. “A realistic quasi-physical model of the 100 m dash.” Canadian Journal of Physics 79.4 (2001): 697-713.