Wat pakt het beste uit bij tennis: Dubbele fouten vermijden door voorzichtig te serveren, of juist wat meer risico nemen zodat de tegenstander meer moeite heeft om de bal terug te slaan? Met behulp van wiskunde kun je de optimale servicestrategie bepalen. En dan blijkt dat we veel toppers een tip kunnen geven: Wees wat minder voorzichtig.

Bij tennis wordt de bal met een opslag in het spel gebracht. Beide spelers mogen om en om een game lang serveren. In tegenstelling tot veel andere sporten zoals volleybal en badminton mogen spelers twee servicepogingen doen. Een eerste service, en als die fout is, een tweede service. Is de tweede service ook fout, een dubbele fout, dan gaat het punt direct naar de tegenstander. De meeste spelers nemen meer risico met de eerste service door de bal wat harder te slaan, of meer op de hoek van het servicevak te richten. Is de eerste service uit of in het net, dan nemen ze flink minder risico met de tweede service. Maar hoeveel risico is optimaal? Geoff Pollard laat in zijn artikel What is the best serving strategy? de manier zien die hij samen met Graham Pollard heeft bedacht om dit te berekenen.
Om te beginnen moet je weten wat het effect is van meer of minder risico nemen. Stel bijvoorbeeld dat een speler de eerste service 40% van de keren fout slaat. Is de eerste service in, dan heeft hij een goede kans om de rally te winnen, bijvoorbeeld 70%. Bij de tweede service speelt hij meer op safe, die is maar 10% van de keren fout. Maar na een zachtere tweede service daalt de kans om de rally te winnen ook, naar bijvoorbeeld 50%. Wat gebeurt er als je qua risico tussen de eerste en tweede service in gaat zitten, of zelfs meer risico neemt dan met de eerste service? De Pollards gingen op zoek naar een verband tussen risico en de kans om de rally te winnen. In figuur 1 is een mogelijk verband te zien, en zien we ook de twee punten die horen bij de eerste en tweede service uit het voorbeeld. Hoe trek je nu de juiste lijn door deze twee punten?
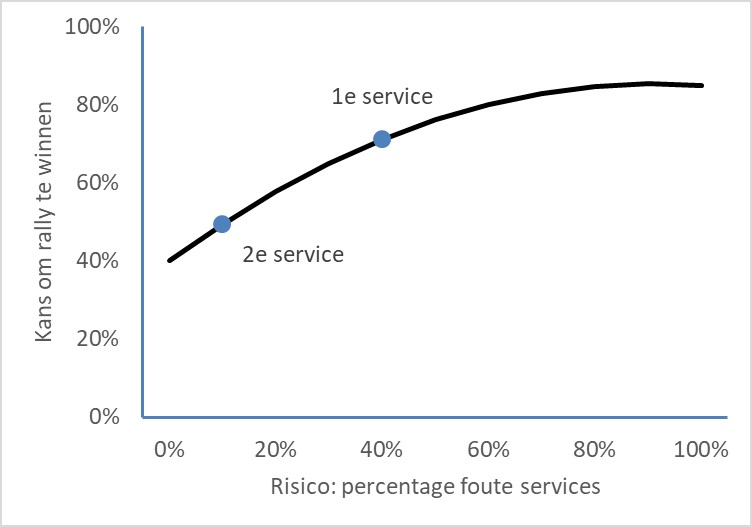
Figuur 1: Voorbeeld van een verband tussen de hoeveelheid risico en de kans om de rally te winnen na een goed geslagen service.
Het meest eenvoudige is om uit te gaan van een rechte lijn. Maar Geoff en Graham Pollard analyseerden veel wedstrijden op professioneel niveau, en kwamen erachter dat dat niet kan kloppen. De lijn gaat op een gegeven moment afvlakken, net als in de figuur. Meer risico nemen levert steeds iets minder op.
Stel dat we weten hoe de lijn loopt. Hoe kunnen we dan de optimale hoeveelheid risico berekenen? We moeten dan eerst weten hoe de kans om het punt te winnen als je serveert afhangt van de hoeveelheid risico op de eerste service en de tweede service. Er zijn twee manieren om een punt te winnen. De eerste mogelijkheid is dat de eerste service in is, en je daarna de rally wint. De tweede optie is dat de eerste service fout is, de tweede service goed, en je daarna de rally wint. Met behulp van de grafiek uit figuur 1 kun je de kans berekenen om het punt te winnen op basis van de gespeelde eerste en tweede service. Maar je kunt ook kijken wat er gebeurt als we de blauwe punten naar links of naar rechts laten lopen over de zwarte lijn. Met behulp van wiskunde kun je bepalen hoeveel risico tot een zo hoog mogelijke kans leidt om het punt te winnen.
Laten we dit eens toepassen om een echte wedstrijd, en kijken of we toptennissers advies kunnen geven. Op 14 juli speelden Novak Djokovic en Roger Federer de finale van Wimbledon tegen elkaar. Het was een enorm lange en spannende wedstrijd. Na vijf uur spelen won Djokovic met 7-6, 1-6, 7-6, 4-6, 13-12. In tabel 1 zijn de wedstrijdstatistieken te zien, die te vinden zijn op www.flashscore.nl.

Tabel 1: Wedstrijdstatistieken van de finale op Wimbledon tussen Djokovic en Federer.
Beide spelers sloegen in meer dan 60% van de gevallen hun eerste service goed. De tweede service was rond de 90% van de keren goed. Ondanks dat Federer verloren heeft zien zijn statistieken er wat beter uit. Hij wint vaker de rally als zijn service goed is. In totaal heeft hij ook net wat meer punten gewonnen dan Djokovic, mede dankzij de tweede set die hij dik heeft gewonnen.
Laten we de eerste en tweede service van de spelers in een grafiek zetten, en er op de manier van Pollard en Pollard een lijn doorheen trekken. Als we de lichtgroene punten in figuur 2 over de stippellijn laten bewegen blijkt dat het optimaal is om ze wat naar rechts te verschuiven. Beide spelers hadden beter meer risico kunnen nemen op zowel de eerste als tweede service!
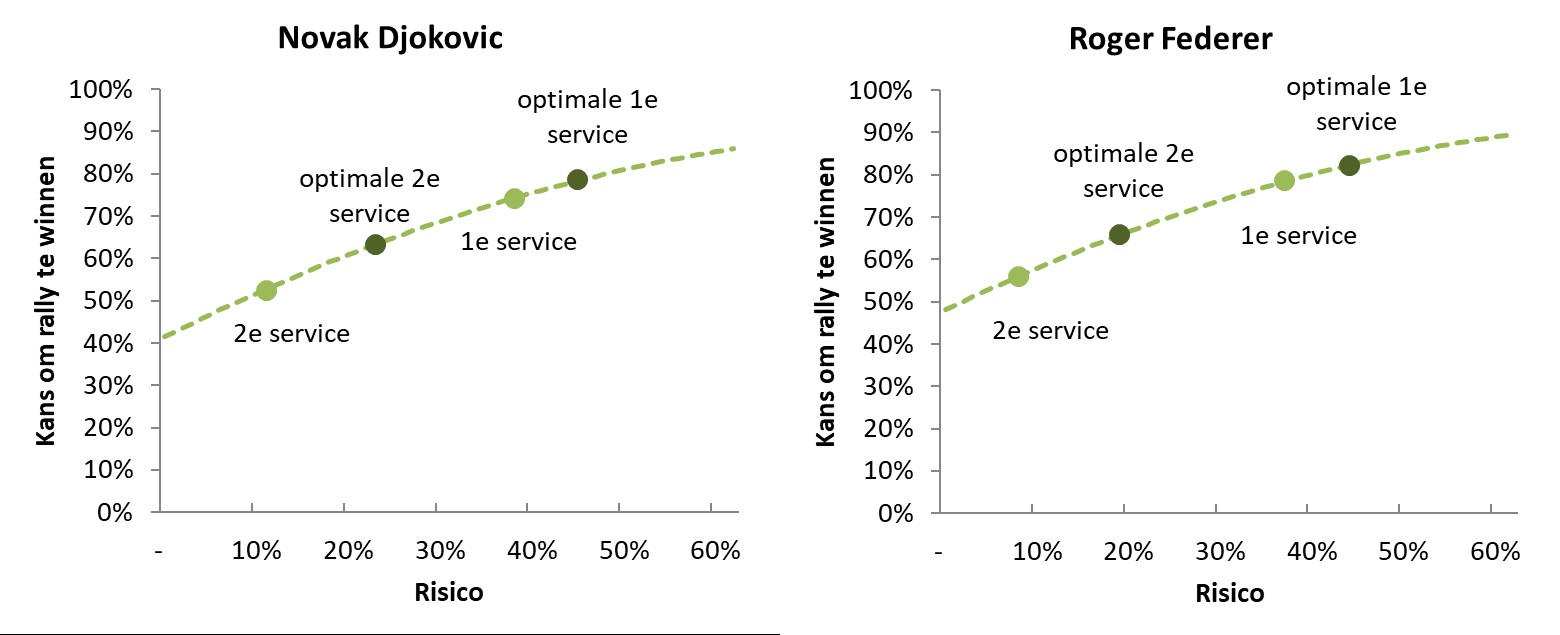
Figuur 2: Verband tussen risico en kans om de rally te winnen voor beide spelers op basis van de wedstrijdstatistieken.
Als ze de optimale strategie gebruiken stijgt de kans om het punt te winnen op eigen service met ruim een procent. Dat lijkt misschien niet veel, maar als je bedenkt dat Federer twee matchpoints heeft gehad op eigen service, dan telt elke procent. Op topniveau gaat het om kleine verschillen.
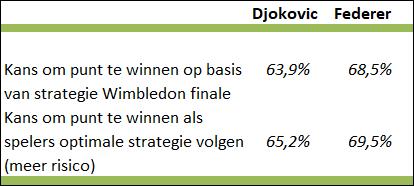
Tabel 2: Kans om het punt te winnen op eigen service op basis van werkelijke en optimale strategie.
Moeten de spelers deze strategie meteen toe gaan passen? We moeten voorzichtig zijn met het aanpassen van de eerste service. De optimale eerste service ligt buiten de twee punten op de grafiek die uit de wedstrijd volgen, we hebben ‘geëxtrapoleerd’. De uitkomst is daarom vrij gevoelig voor de manier waarop je de lijn precies laat afvlakken. Maar als we op deze manier meer wedstrijden analyseren, ook met verschillende manieren om een lijn door de twee punten te trekken, komt één conclusie vaak terug: Spelers zouden meer risico moeten nemen met hun tweede service, en de extra dubbele fouten voor lief moeten nemen. Er zijn zelfs wedstrijden waarbij een van de twee spelers de tweede opslag beter als een eerste opslag had kunnen slaan. Waarom doen ze dat dan niet? Waarschijnlijk zijn ze te bang om het punt gelijk te verliezen met een dubbele fout, ook al laat wiskunde zien dat dat onterecht is.
Wil je voor meer wedstrijden zien hoe dit uitpakt? Kijk dan eens naar deze app.