Wiskundigen hebben berekend hoe je de getallen 1 tot 20 zo goed mogelijk over het dartbord kan verdelen. Dit leidt tot een net iets ander dartbord dan het huidige dartbord, waarin even en oneven getallen elkaar afwisselen. Mooie bijvangst: Analyses verklaren ook waarom er relatief weinig linkshandige topdarters zijn. Het huidige bord werkt namelijk in hun nadeel.
Het huidige dartbord is in 1896 bedacht door Brian Gamlin. Het idee erachter was dat hoge getallen vaak naast lage getallen staan. Zo staat de 20 naast de 1 en de 5. Als je op de 20 mikt en mist wordt dat dus relatief zwaar bestraft. Er zit verder geen volledige logica achter, naast de 20 had net zo goed een 2 of een 3 kunnen staan. Dat triggert wiskundigen. Ze willen het liefst op basis van één of meerdere criteria het dartbord optimaliseren. Veel wiskundigen hebben hier al onderzoek naar gedaan. Het meest recente onderzoek komt van David Percy uit 2012. Zijn optimale dartbord is hieronder te zien.

Figuur 1: Links: Huidig dartbord. Rechts: Optimale dartbord volgens Percy.
Het nieuwe bord is gebaseerd op drie criteria:
- Bestraf fouten van spelers die op hoge getallen richten.
- Wissel even en oneven nummers af.
- Zorg dat de verwachte score per plek op het bord ongeveer hetzelfde blijft als je het bord een stuk draait.
Het eerste criterium is ook in eerdere onderzoeken gebruikt, en is ook het idee achter het bord van Gamlin. Als je op de 20 mikt en mist wordt je harder bestraft dan wanneer je op bijvoorbeeld de 14 mikt. Het tweede criterium is oorspronkelijk bedacht door Rob Eastaway en John Haigh. Bij darts moet je een score van 501 behalen om een leg te winnen. Op een gegeven moment moet je dus een oneven getal raken. Als je oneven en even getallen afwisselt, bestraf je het ook weer extra als een darter z’n doel mist. Op het huidige bord zitten een aantal clusters van oneven getallen, bijvoorbeeld 17,3,19 en 7. Ook zit de 16 naast de 8, dit is weer in strijd met criterium 1. Als je 32 over hebt en je gooit in plaats van dubbel 16 een enkele 16, dan is het relatief makkelijk om op de dubbel 8 er vlak boven te richten. Als derde criterium voegt Percy toe dat de verschillende plekken op het dartbord ongeveer even hoge scores moeten geven, zodat geluk een zo klein mogelijke rol speelt. Op het huidige dartbord zitten bijvoorbeeld 12, 9 en 14 naast elkaar (gemiddeld 11,7) en 16, 7 en 19 (gemiddeld 14). Hij wil die verschillen verkleinen.
Het meeste onderzoek voor Percy concentreerde zich op het eerste criterium. Hoge en lage getallen moeten elkaar afwisselen. Dit werd gedaan door te kijken naar de absolute verschillen tussen opeenvolgende getallen. Zo kun je kijken naar de som van de absolute verschillen van het huidige bord:
|20-1|+|1-18|+…|5-20|=19+17+…+15=198
Of je sommeert de absolute verschillen in het kwadraat:
|20-1|2+|1-18|2+…|5-20|2=192+172+…+152=2478
Singmaster heeft een dartbord bedacht waarbij de som van de absolute verschillen in het kwadraat maximaal is:
(20, 1, 19, 3, 17, 5, 15, 7, 13, 9, 11, 10, 12, 8, 14, 6, 16, 4, 18, 2)
De som is dan gelijk aan |20-1|2+|1-19|2+…|2-20|2=192+182+…+182=2642
Nadeel van dit bord is echter dat de oneven en even getallen elkaar niet afwisselen. Sterker nog, alle oneven en even getallen staan naast elkaar. Je kunt dus niet alle drie de criteria tegelijk optimaliseren. Percy kwam daarom met een nieuwe methode die de optimale balans tussen de drie voorwaardes zoekt. Hij kijkt niet naar het verschil van twee opeenvolgende getallen, maar naar de som. Die som is gemiddeld 21. Onder de voorwaarde dat even en oneven getallen elkaar afwisselen zorgt hij dat de som van twee getallen naast elkaar altijd zo dicht mogelijk bij 21 ligt. Het is mogelijk om een bord te maken zodat de som altijd gelijk is aan 19, 21 of 23. Los van draaiingen en spiegelingen van het bord is hier maar één mogelijkheid voor. De 20 moet tussen de 1 en de 3. De 1 moet tussen de 20 en de 18. De 18 moet naast de 1, 3 of 5. De 3 zit al naast de 20, dus volgt na 20, 1 en 18 de 5. Op basis van deze logica kun je het hele dartbord rondgaan en kom je uit op het bord van Percy. De som van twee opeenvolgende getallen wijkt altijd maximaal 2 af van 21. Resultaat: Een dartbord met afwisselend oneven en even getallen, hoge getallen naast lage getallen, en een verwachte score die ongeveer gelijk blijft als je het bord een stukje draait.
Dan naar de linkshandige topdarters. Wereldwijd is ongeveer 10% van de mensen linkshandig. In 2014 deden 128 darters meer met de PDC Pro Tour, en maar 5 daarvan waren linkshandig. Dit is 4%, veel minder dan de 10% die je ongeveer zou verwachten. Jack Peacock, Jeshua Maxey en Vijay Tymms zoeken de verklaring in de opzet van het dartbord. In dit artikel kon je lezen hoe je de verwachte score per plek op het dartbord kunt bereken, afhankelijk van hoe nauwkeurig je kunt gooien. Ook zagen we daar dat de pijl van rechtshandigen vaker linksboven en rechtsonder hun doel terechtkomt. Bij linkshandigen is het precies andersom. In figuur 2 is een typisch patroon te zien van een linkshandige en rechtshandige speler die mikt op de Bullseye.
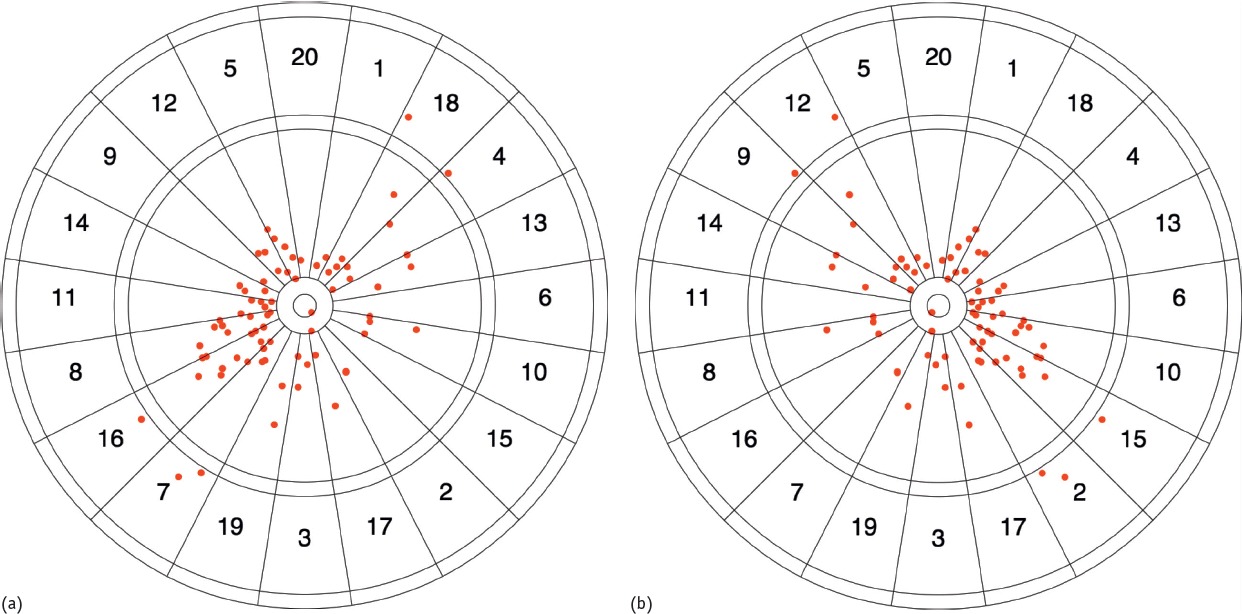
Figuur 2: Darts van linkshandige speler (a) en rechtshandige speler (b) die mikt op de Bullseye. Bron: Peacock, Maxey en Tymms (2015).
Waarom is het huidige bord in het nadeel van linkshandigen? Als we kijken naar de vorm van de hoge dubbels, bijvoorbeeld de dubbel 16, 18 en 19, sluit de vorm van de dubbels veel beter aan bij het patroon van de rechtshandige spelers. Als een rechtshandige speler mikt op het midden van de dubbel, en de pijl komt een klein stukje linksboven of rechtsonder het midden terecht, zit de pijl nog steeds in het juiste vakje. Komt de pijl echter rechtsboven of linksonder het midden, dan zit hij er veel eerder buiten. James Wade, een van de beste linkshandige spelers eindigt vaak met een dubbel 10. Die sluit beter aan bij het patroon van een linkshandige. De onderzoekers hebben berekend dat de verwachte score per pijl voor linkshandigen bijna 7% lager ligt als ze even nauwkeurig kunnen gooien. Bij het dartbord van Percy zijn deze verschillen veel kleiner.
Nou, invoeren dat dartbord, toch? De BDO heeft geëxperimenteerd met het nieuwe bord, maar daar is het bij gebleven. Op dit moment zijn er geen plannen om het huidige bord te vervangen. Misschien moeten we maar met iets meer respect kijken naar James Wade en Mark Webster als ze de volgende keer staan te gooien.
Bronnen:
Eastaway, R., & Haigh, J. (2014). The hidden mathematics of sport. Pavilion Books.
Peacock, J., Maxey, J., & Tymms, V. (2015). Left out?. Significance, 12(2), 36-39.
Percy, D. F. (2012). The optimal dartboard?. Mathematics Today, 48(6), 268-270.










Gave blog! Goede analyse en heerlijk geschreven. Dankje.
Dank je!
Pingback: Linkshandig? Ga schermen maar niet darten | Sport & statistiek