In het tijdschrift STAtOR heb ik een vervolgonderzoek gepubliceerd. Het artikel is hier te vinden.
Augustus vorig jaar werd Dafne Schippers wereldkampioen op de 200 meter sprint. Nu “we” meedoen op deze afstand, neemt de belangstelling toe. Zou ze deze zomer ook Olympisch kampioen kunnen worden? Ook door een natuurkundige en wiskundige bril is deze afstand interessant. De wetenschap heeft van alles te zeggen over de invloed van hoogte, luchtdruk, wind, en het effect van de laan waarin de atleten loopt.
De 200 meter
Bij baanatletiek lopen atleten op een 400 meter baan. De baan bestaat uit twee rechte stukken van ongeveer 100 meter, en twee bochten. De atleten lopen naast elkaar in 4 tot 9 lanen. De binnenste laan, laan 1, loopt een kortere bocht dan de buitenste laan. Daarom starten de atleten niet naast elkaar, maar mag de buitenste laan verder naar voren starten, zodat ze als ze over de finish komen, allemaal precies 200 meter hebben afgelegd.
Op een groot toernooi worden er eerst series gelopen, waar de sprinters zich kunnen plaatsen voor de halve finales en de finale. In de eerste serie krijgen de atleten willekeurig een laan toegewezen. Atleten die de snelste tijd hebben gelopen in de series, starten in de volgende ronde in de binnenste lanen (4 en 5). Het is voordelig om een ruimere bocht te lopen, want dit kost minder kracht. Het is dus nadelig om in laan 1 te starten. Bij indoor atletiek is de baan 200 meter in plaats van 400 meter, en lopen de atleten dus een volle ronde. Het nadeel van een krappere bocht is hier zo groot, dat deze afstand bij indoortoernooien van het programma is gehaald.

De beste tijd ooit?
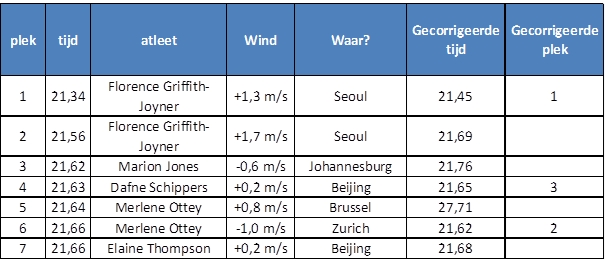
Dafne Schippers werd vorig jaar niet alleen wereldkampioen, maar werd met 21,63 seconde ook de derde snelste atlete ooit. Alleen Florence Griffith-Joyner (21,34) en Marion Jones (21,62) waren sneller. Wat zijn de ideale omstandigheden om een snelle tijd te lopen? Het is vanwege de bocht dus voordelig om in de buitenste laan te starten. Maar ook de luchtdruk speelt een rol. Hoe hoger de luchtdruk, hoe hoger de luchtweerstand, en hoe moeilijker het is om een snelle tijd te lopen. Dit effect is ook heel duidelijk bij schaatsen. Daar worden wereldrecords altijd gereden op hooglandbanen zoals Calgary en Salt Lake City, waar de luchtdruk laag is. Omdat het zo goed als onmogelijk is om dezelfde tijd te rijden op een laaglandbaan, zijn hier zelfs officieuze aparte wereldrecords voor. Ook helpt het natuurlijk als je wind mee hebt. Bij atletiek is een wereldrecord daarom pas officieel als de windsnelheid minder dan 2 meter per seconde is. En vanwege het voordeel van een hoogland baan, komt er bij een baan die hoger dan 1000 meter boven zeeniveau ligt een A achter het wereldrecord te staan.
Jonas Mureika, een professor natuurkunde in Los Angeles, heeft een model ontwikkeld waarmee hij het effect van luchtdruk, mee- of tegenwind en de startlaan heeft geschat. De kern van het model is een formule die je misschien nog kent van de natuurkundelessen van de middelbare school: F=m*a. Kracht is massa keer versnelling, de beroemde tweede wet van Newton. Een sprinter oefent kracht uit, om te versnellen, en zo snel mogelijk te lopen. Er zijn ook krachten buiten de atleet die meewerken of tegenwerken. De luchtweerstand moet overwonnen worden, en hoe hoger de luchtdruk, hoe groter deze tegenkracht. Ook tegenwind kan tegenkracht geven, en meewind een extra duwtje in de rug. Als laatste is ook het effect van de bocht in een kracht te vatten. Als je de bocht ziet als een halve cirkel, moet de atleet een kracht uitoefenen richting het middelpunt van de cirkel, om de bocht te lopen, de middelpuntzoekende kracht. Hoe kleiner de straal van de cirkel is, hoe groter deze kracht is, en daarom is het nadelig om de binnenbocht te lopen. Op zijn website kun je de 200 meter tijd bepalen die corrigeert voor deze drie effecten. Op basis daarvan zou je een nieuwe ranglijst van beste atletes ooit kunnen maken. Dafne Schippers blijft dan op de derde plek staan, alleen moet Marion Jones haar tweede plek afstaan aan Merlene Ottey. Jones liep 21,62 in Johannesburg, en Ottey 21,66 in Zurich. Ottey had meer tegenwind dan Jones, Zurich ligt op 400 meter hoogte, en Johannesburg op 1700 meter. Twee factoren waardoor de tijd van Ottey naar beneden wordt bijgesteld, en die van Jones naar boven.
Statistiek en het effect van de startlaan
(inmiddels heb ik vervolgonderzoek gedaan naar het effect van de startlaan. De link naar dat artikel is bovenaan te vinden).
De tijd die een atleet loopt wordt dus beïnvloed door de hoogte, wind en de startlaan. De hoogte en de wind zijn voor alle atleten in een wedstrijd hetzelfde. Maar het effect van de startlaan geeft de atleet in de buitenste laan een voorsprong op de atleet die in de binnenste laan start. Is dit ook terug te zien in de resultaten op een wereldkampioenschap? In de eerste ronde krijgen de atleten willekeurig een startlaan toegewezen. Het zou dan zo moeten zijn dat atleten in laan 8 zich significant vaker voor de volgende ronde kwalificeren dan atleten in laan 1. Om dat te testen bekijken we alle series van wereldkampioenschappen atletiek outdoor vanaf 1991, en de Olympische Spelen vanaf 2000. Atleten die gediskwalificeerd werden, of de finish niet bereikten zijn weggelaten.
In de figuren hieronder is voor alle combinaties van startlaan en eindklassering te zien hoe vaak die voorkwam. Zo zijn er bijvoorbeeld 23 mannen geweest die startten in laan 5 en als eerste eindigden. En waren er 5 vrouwelijke atletes die startten in laan 5 en als 8e eindigden. Bij de meeste kwalificaties plaatsen de eerste drie atleten zich voor de volgende ronde. We kunnen nu uitrekenen hoe vaak een atleet zich kwalificeerde, afhankelijk van de startlaan. En dan zien we opmerkelijke verschillen. Bij de mannen kwalificeert maar 23% van de atleten in laan 1 zich, tegenover bijvoorbeeld 50% in laan 4. Ook bij de vrouwen valt op dat atletes in laan 1 zich minder vaak plaatsen voor de volgende ronde.
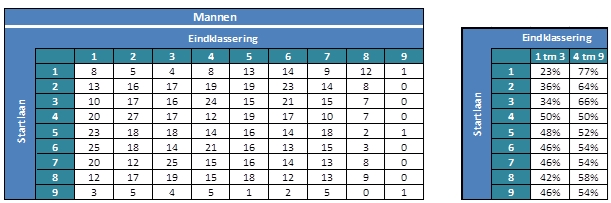
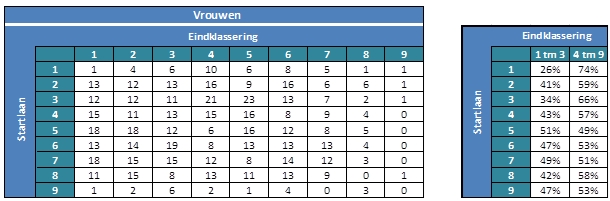
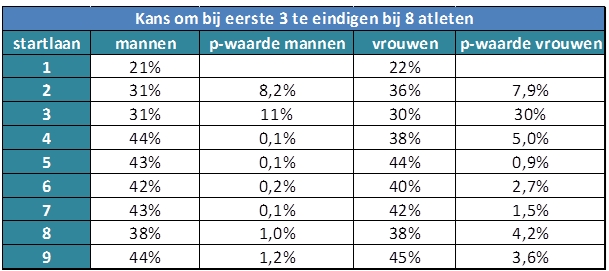
Het kan natuurlijk zijn dat dit door toeval wordt veroorzaakt. Ook starten niet in elke serie evenveel atleten. Een manier om te testen of het verschil op toeval kan berusten is door een zogenaamd Generalized Linear Model te schatten. Hierbij corrigeren we eerst voor het aantal atleten dat meedoet aan een serie. Vervolgens schat het model de kans dat een atleet bij de eerste drie eindigt, afhankelijk van de startlaan, als er acht atleten mee zouden doen. Ook bepaalt het model hoe groot de kans is dat verschillen op toeval berusten. In de tabel hieronder zijn de resultaten te zien. Als er geen effect van startlaan was, zou de kans om bij de eerste drie te eindigen altijd ongeveer 3/8=37,5% moeten zijn. In laan 1 ligt deze kans nog steeds een stuk lager, zowel voor mannen als voor vrouwen. Ook in laan 2 en 3 ligt de kans om bij de eerste drie te eindigen onder de 37,5%. De kolom met de p-waarde berekent de kans dat verschillen tussen startlanen door toeval ontstaan. Hierbij wordt een startlaan altijd vergeleken met laan 1. Meestal wordt een grens van 5% gehanteerd. Pas als de p–waarde kleiner is dan 5%, gaan we er vanuit dat verschillen niet op toeval berusten. We noemen het effect dan statistisch significant. Voor laan 2 en 3 is de kans dat een atleet zich plaatst niet significant anders ten opzichte van laan 1. Voor laan 5 tot en met 9 wel. De startlaan heeft dus een statistisch significant effect op de kans dat een atleet zich plaatst voor de volgende ronde.
Conclusie
De tijd die een atleet loopt op de 200 meter wordt beïnvloed door wind, hoogte en de laan waarin de atleet start. Op basis van een natuurkundig model kunnen tijden op verschillende hoogtes en bij verschillende windsnelheden met elkaar vergeleken worden. Marion Jones moet haar positie als tweede snelste vrouw ooit dan afstaan aan Merlene Ottey. Starten in de binnenste laan levert een nadeel op, dat statistisch aangetoond kan worden.
Mureika, J. R. “Modeling wind and altitude effects in the 200 m sprint.” Canadian Journal of Physics 81.7 (2003): 895-910.
Mureika, J. R. “A realistic quasi-physical model of the 100 m dash.” Canadian Journal of Physics 79.4 (2001): 697-713.