Speltheorie geeft wiskundige principes die je toe kunt passen op tennis om de optimale serveer- en ontvangstrategie te bepalen. Maar volgen toptennissers ook deze regels? Behoorlijk goed, blijkt uit een analyse van ruim 3000 wedstrijden op Wimbledon. En de spelers met een hoge ranking doen dit beter dan de subtoppers.
John Forbes Nash was een wiskundige die veel mensen zullen kennen van de film A beautiful mind. Daarin is te zien hoe hij worstelt met zijn schizofrenie en hallucinaties. Ondanks zijn problemen heeft hij een enorme bijdrage geleverd aan de wetenschap. Dit levert hem in 1994 de Nobelprijs voor de economie op voor zijn onderzoek op het gebied van speltheorie. Speltheorie houdt zich bezig met het bepalen van de optimale strategie bij een “spel” met twee of meer spelers. Het begrip “spel” moet ruim opgevat worden. Het kan daadwerkelijk gaan over een spel zoals Stratego. Maar ook om bijvoorbeeld het vaststellen van de prijs van een product om zoveel mogelijk winst te maken. Bij speltheorie gaat men ervan uit dat de spelers zich rationeel gedragen en wiskundig gezien de optimale beslissing nemen. In de praktijk blijkt dit niet altijd zo te zijn.
Speltheorie is ook toe te passen op sporten zoals tennis en voetbal. Bij voetbal kun je bijvoorbeeld berekenen wat de optimale strategie is als je een penalty neemt. Wellicht heeft degene die de penalty neemt een favoriete hoek. Hij maakt de meeste kans om te scoren als hij naar links schiet. Maar als de keeper dat weet dan zal hij daar al op inspelen en altijd naar links duiken. De speler zal daarom ook af en toe naar rechts schieten. Op dezelfde manier kunnen we naar de service van tennissers kijken. Soms slaat hij de service naar buiten, en soms naar binnen. Ook de ontvanger speelt van tevoren al een beetje in op een richting. Wat is de optimale strategie voor de serveerder en ontvanger, en houden spelers zich daaraan? Om dat te onderzoeken analyseerden Romain Gauriot, Lionel Page en John Wooders ruim 3000 wedstrijden op Wimbledon in hun artikel Nash at Wimbledon: Evidence from Half a Million Serves.
Laten we eerst eens aan de hand van een voorbeeld bekijken hoe je de optimale strategie kunt bepalen. We gaan uit van een vereenvoudigde situatie. Degene die serveert heeft één servicemogelijkheid en serveert naar buiten of naar binnen (langs de T). De ontvanger kan ook alvast gokken of voorsorteren op een service naar buiten of naar binnen, bijvoorbeeld door iets meer richting een bepaalde kant van het veld te gaan staan. In de meest vereenvoudigde situatie zijn er vier mogelijkheden. De serveerder slaat naar buiten of binnen en de ontvanger sorteert voor op een service naar buiten of binnen. In de volgende tabel staat per optie een voorbeeldpercentage dat aangeeft hoe groot de kans is dat de serveerder het punt wint. De serveerder heeft meer kans om het punt te winnen als hij naar buiten serveert. Maar hij heeft minder kans om het punt te winnen als de ontvanger goed gokt (buiten-buiten of binnen-binnen) dan wanneer de ontvanger verkeerd gokt (buiten-binnen of binnen-buiten).

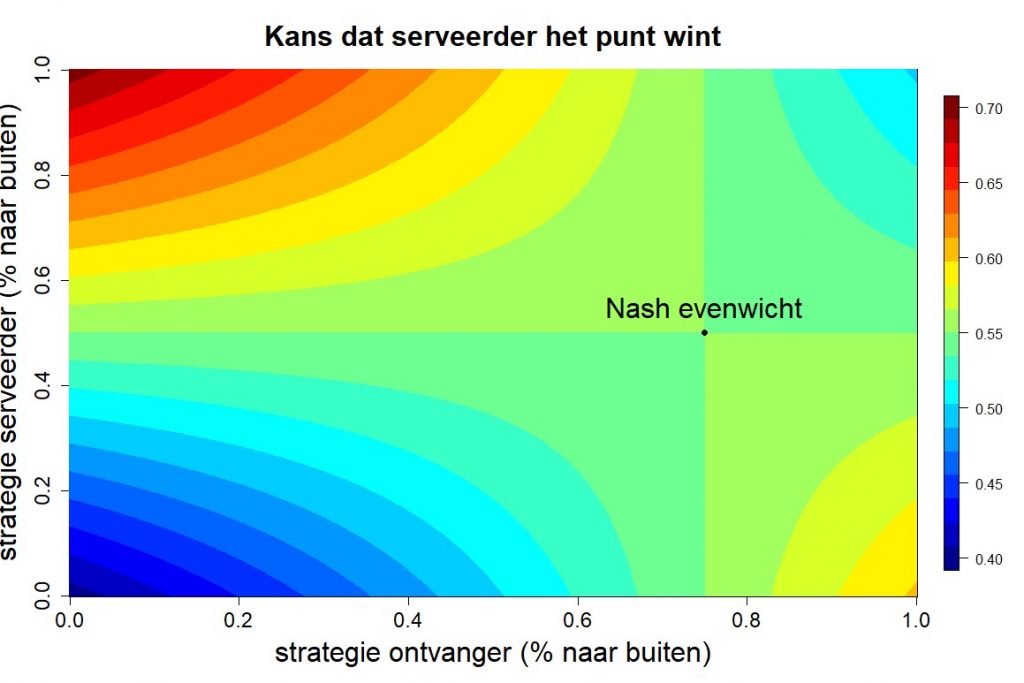
Nu gaan we ervan uit dat zowel de serveerder als de ontvanger een bepaalde strategie gaat volgen. Stel bijvoorbeeld dat de serveerder 50% naar buiten slaat en 50% naar binnen. De ontvanger gokt ook niet volledig op één kant, maar gaat ook uit van 50% naar buiten en 50% naar binnen. We nemen aan dat we de winkansen ook kunnen middelen. Bij een service naar buiten wint de serveerder dan in 60% van de gevallen, bij een service naar binnen in 50% van de keren. In totaal is de kans dat de serveerder het punt wint dan 55%. Die kans kunnen we berekenen voor alle mogelijke strategieën van zowel de serveerder als de ontvanger. Laten we xs de strategie van de serveerder noemen. Dit is het percentage van de opslagen die hij naar buiten serveert. De overige (1-xs) van de services slaat hij naar binnen. De strategie van de ontvanger noemen we xo en die geeft weer in hoeverre hij gokt op een service naar buiten. In de volgende figuur is de winkans van degene die opslaat te zien, afhankelijk van de strategie van beide spelers:
Stel we starten met de strategie van 50/50 voor beide spelers. De serveerder kan dan zijn winkans vergroten door wat vaker naar buiten te serveren. Maar de ontvanger zal daar ook op inspelen door wat meer te gokken op een service naar buiten, om zo de kans van de serveerder te verlagen. Ze zullen net zolang inspelen op elkaars strategie tot er een evenwicht is, het Nash-evenwicht. Het is dan voor beide spelers niet meer voordelig om de strategie aan te passen. Dit evenwicht wordt weergeven met de zwarte stip in de figuur. De serveerder slaat 50% naar buiten en 50% naar binnen. De ontvanger gokt 75% op een service naar buiten. De kans dat de serveerder het punt wint is dan 55%. Als één van de twee spelers de strategie aanpast komt dat overeen met een horizontale of verticale beweging over de figuur. We kunnen zien dat de kans dan 55% blijft. De wiskundige afleiding van dit Nash-evenwicht is in het kader onderaan dit artikel te vinden.
Dit Nash-evenwicht heeft een eigenschap waardoor we relatief eenvoudig kunnen controleren of tennissers de optimale strategie volgen. De kans dat de serveerder het punt wint als hij naar links serveert is gelijk aan de kans dat hij het punt wint als hij naar rechts serveert. Dat kunnen we voor dit voorbeeld narekenen. De ontvanger gokt 75% op een service naar buiten. Als de opslag naar buiten gaat is de winkans voor de serveerder dus 0,75⋅0,5+0,25⋅0,7=0,55. Indien hij naar binnen slaat komt hier hetzelfde uit: 0,75⋅0,6+0,25⋅0,4=0,55. Ook als je meer opties meeneemt, bijvoorbeeld een service op het lichaam, blijft deze eigenschap behouden.
Laten we eens één wedstrijd bekijken, en kijken of er een Nash-evenwicht is. Er is een mooie database waarin mensen wedstrijden punt voor punt hebben gecodeerd. Dit is het Match Charting Project van Jeff Sackermann. Van elke rally wordt bijgehouden wat de slagen waren (b.v. forehand langs de lijn, gevolgd door een backhand cross, winner). Een enorm karwei. In deze data wordt ook per punt aangegeven waar de service terecht is gekomen. Aangezien dit heel veel werk is, worden er maar een beperkt aantal wedstrijden geanalyseerd. Een daarvan is de finale tussen Djokovic en Del Potro op de US Open in 2018. Djokovic won met 6–3, 7–6, 6–4. Laten we kijken naar de eerste services, vanaf links en vanaf rechts.
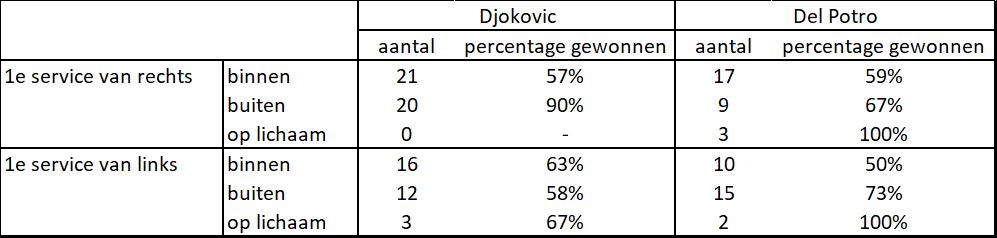
Als Djokovic en Del Potro zich aan de regels van Nash houden, dan zou het percentage gewonnen punten na een service altijd ongeveer gelijk moeten zijn. Als Djokovic van links serveerde in deze wedstrijd, lagen de percentages redelijk dicht bij elkaar. Vanaf rechts scoorde hij echter veel vaker als hij naar buiten sloeg. Volgens Nash had dat ertoe moeten leiden dat Djokovic vaker naar buiten had moeten serveren, of dat Del Potro meer voor had moeten sorteren op een service naar buiten. Bij Del Potro valt op dat hij opvallend goed scoorde als hij een service op het lichaam speelde. Het leidde altijd tot puntwinst. Dit deed hij in totaal echter maar vijf keer, dus dit kan ook toeval zijn.
Romain Gauriot, Lionel Page en John Wooders onderzochten ruim 3000 wedstrijden op Wimbledon om uit te zoeken of er tijdens deze wedstrijden een Nash-evenwicht was. Daardoor kunnen ze betrouwbaardere conclusies trekken. Ze konden gebruik maken van data van het Hawk-Eye systeem. Camera’s volgen precies waar elke bal terecht komt. Tennissers mogen een aantal keer per wedstrijd een beslissing van de scheidsrechter ter discussie stellen. De baan van de bal wordt dan afgespeeld op een scherm in het stadion, om te kijken of de bal daadwerkelijk in of uit was. De onderzoekers testten met behulp van de data of er een Nash-evenwicht was. Ze keken apart naar de eerste en tweede service, en services van links en rechts. Ze concludeerden dat tennissers vrij goed de optimale strategie volgen. Oftewel, de winkans van de serveerder is min of meer gelijk, onafhankelijk van de kant waarop geserveerd wordt. Mannen volgden de optimale strategie beter dan vrouwen, en hooggeplaatste spelers beter dan lager geplaatste spelers. Een mooie conclusie: De echte toppers zijn betere wiskundigen!

Bronnen:
Gauriot, R., Page, L., & Wooders, J. (2016). Nash at Wimbledon: evidence from half a million serves. Available at SSRN 2850919.
https://github.com/JeffSackmann/tennis_MatchChartingProject